Chatbot Arena in a nutshell

Disclaimer: All of the following content are public information.

Academic Evals are Cracked

It all starts with the question: How do you evaluate the quality of something that’s as strong as GPT-4 (or Gemini).

Before the era of large language model, various of researchers spend many times constructing evaluation benchmark to evaluate the model’s capability progress. I’d argue that a good benchmark is what drive progress in the field of NLP, and claiming the lead on a benchmark usually comes with fame and fortune, driving researchers and companies to compete with each other to create a better model.

However, a lot of the benchmarks proposed in recent years are saturating in an unexpected speed. Take the following diagram as an example, it takes quite some time for a model to hill climb to human level performance in the first 15 years of this century, but just a few years (or months) for some of the newly proposed tasks such as GLUE.

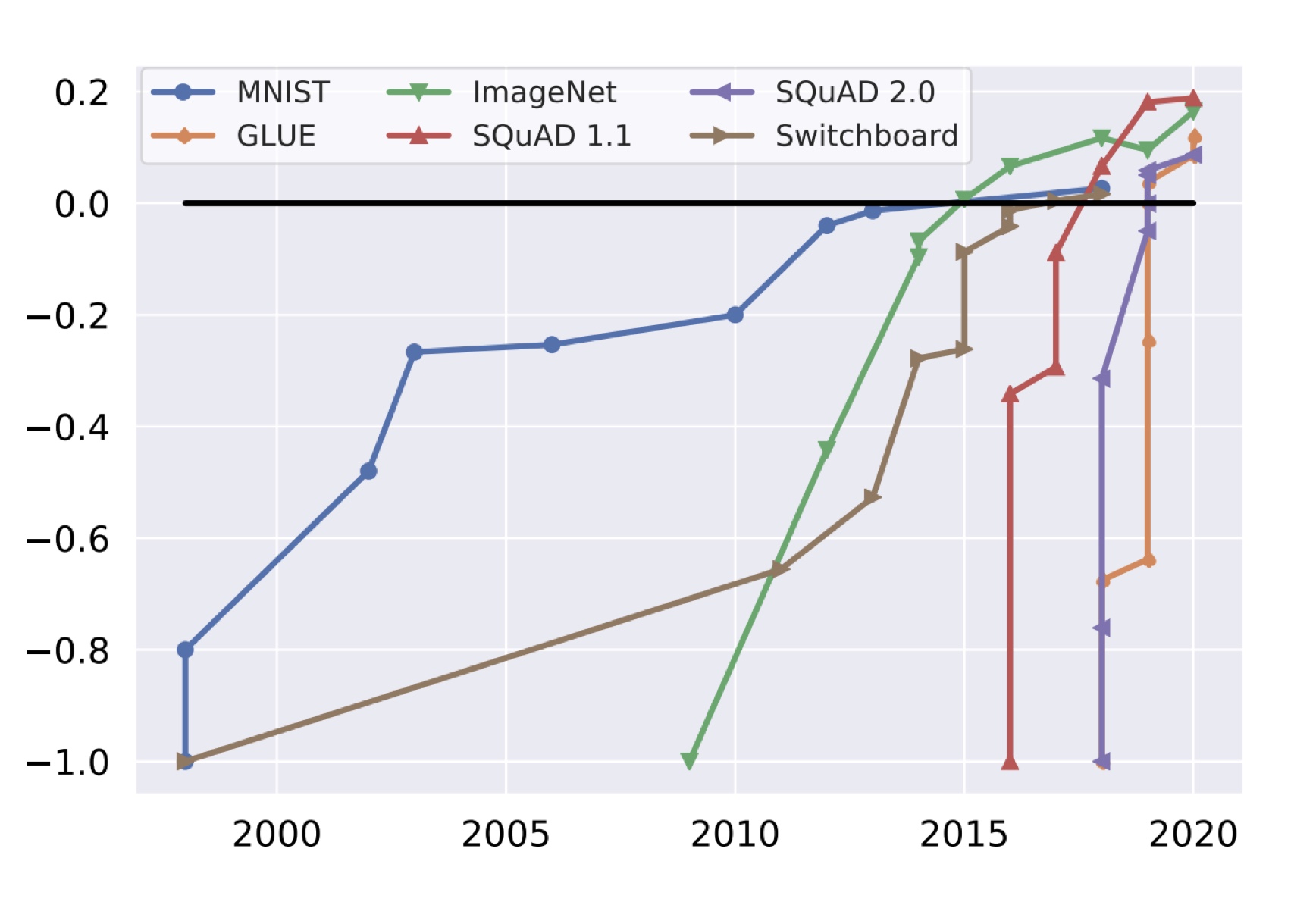
Saturating is just one side of things. Another very annoying issue is leakage. It’s actually quite easy to claim to the top of one leaderboard: You just train on the evaluation dataset. Such training can be intentional, we all know that there are enough dumb VCs who will just dumping money on you if you create a big headline on some leaderboard. But many times, the leakage is implicit and unintentional, with the massive training data, it’s quite common that you scraped some 3rd party website that happen to include a large chunk of MMLU data and by pretraining on it your model just remembers the answer. There are ways to detect such leakage, for example one way of detecting such leakage is by measuring the model’s perplexity on the eval set, and if model is more confident than some threshold we deem the eval set is leaked.

Another solution is to create benchmark that’s either hidden or dynamic. For example, ScaleAI has SEAL leaderboard on which they constantly conduct evaluation to measure the model’s capability. But as ScaleAI is also creating data for all these large language model providers, it’s not so convincing that they will actually adversarially exposing their clients model weakness. Another type of evaluation is to make it dynamic, with periodic refresh of the problem. LiveCodeBench is such a project where new problems are published constantly to ensure the freshness of data.

However, even if we spend a lot of effort curating a very good dataset, we still face a quite serious problem: all of the aforementioned evaluations are quite artificial. A normal user doesn’t just go to LLM to ask leetcode questions, or asking a high school math selection problems. A user’s goal for the LLM is quite simple: ask real life questions and want a high quality answer. How can we make the evaluation focus on this front, while it’s quite challenging to effectively measure the open-ended answers?

Chatbot Arena in a nutshell

Right after ChatGPT released, a few students in Berkeley Sky Computing Lab started to replicate ChatGPT’s success by creating an open source large language model called Vicuna. During the development of Vicuna, they started to realize it’s quite hard to comprehensively evaluate the large language model. To solve this issue, they began to develop an open platform that will later become Chatbot Arena, with a simple hypothesis: “human are good at judging quality of LLM if presented side by side”.

When the user comes to the website, they can issue queries just like using any LLM provider. The query will be sent to 2 “random” LLMs to get responses. And then presented to the user for rating out of 4 options: 1) left is better. 2) right is better. 3) tie. 4) tie (both bad).

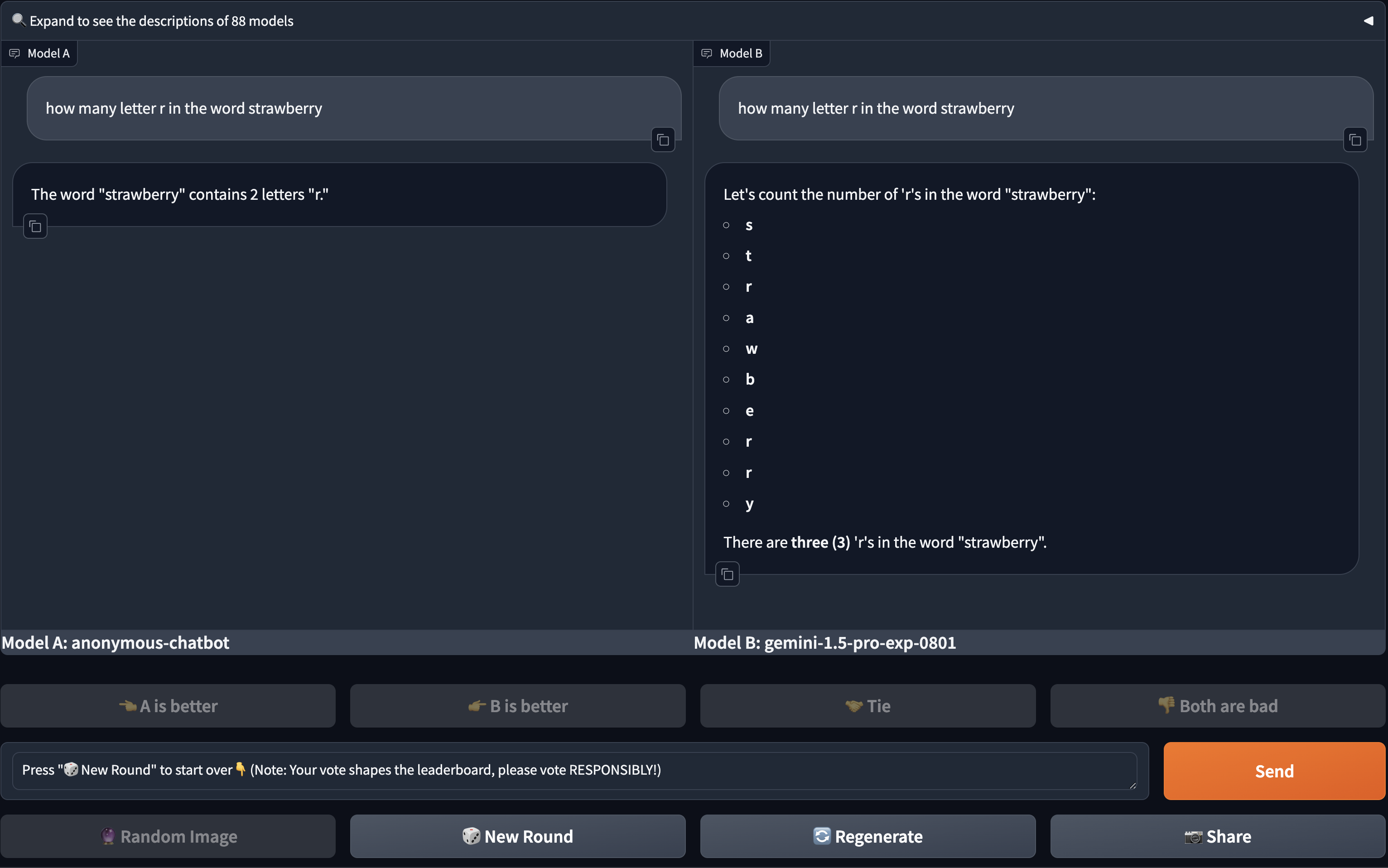
After this rating steps. Arena will gather all the votes and rank the LLMs under comparison. How? Fortunately, human is a competitive animal, and we have already developed many ways to rank stuff. One of the most commonly used ranking systems is ELO ranking. Assuming 2 players in a zero sum game with ELO score \(R_A\) and \(R_B\). The probability of player \(A\) wins over player \(B\) is expressed as:

$$ \begin{equation} \begin{aligned} P(A > B) &= \frac{1}{1 + 10^{(R_B-R_A)/400}} \end{aligned} \end{equation} $$

By looking at all the comparisons submitted by users, we can derive one score for each model to best approximate the above probability. The following leaderboard is derived at 2024-08-11. As shown in Equation (1), the probability of Gemini-1.5-Pro-Exp-0801 being greater than GPT-4o-2024-05-13 is 51.87%¹

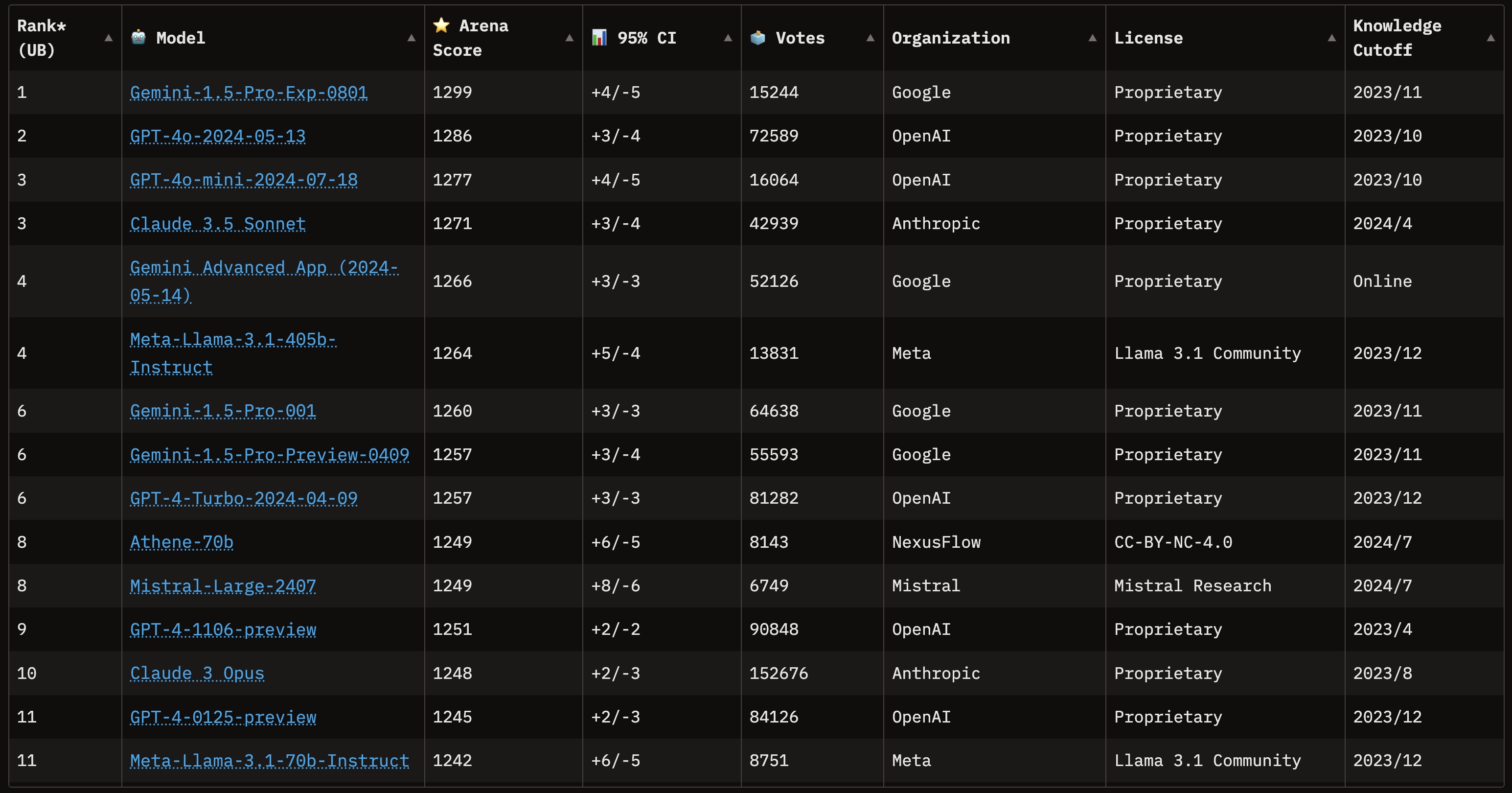
As of the time of writing, this platform has collected comparisons across 127 different models, and a total votes of 1,610,507, and it has become the #1 trusted leaderboard for comparing and understand the strength of all the LLMs. There has been changes to this leaderboard such as introducing hard categories, multi-modal but the core idea is similar. That’s it about Chatbot Arena! A single open platform that open internet users can come and rate LLM on their questions, and a unified leaderboard to rank LLMs by their capabilities!

You don’t know Chatbot Arena

What’s more to understand this leaderboard besides it’s a comparison platform and some magics to calculate the scores? I’d argue that there are many more details in the implementation of this leaderboard and can provide you insights on why some phenomenon exist. Most of the content below is my takeaway after reading their 2024 ICML paper.

Understand the meaning of the score

First, what does Arena score actually mean? Let’s take the leaderboard as an example. Gemini has an Elo score of 1299, while Claude 3.5 Sonnet has an Elo score of 1271. The actual meaning of these 2 score can be translated with equation (1) we derived above. That is,

$$ \begin{aligned} P(\textbf{user prefer Gemini than Claude}) &= \frac{1}{1 + 10^{(R_{claude}-R_{gemini})/400}} \\ &= \frac{1}{1 + 10^{(1271-1299)/400}} \\ &= 0.54 \end{aligned} $$

In another words, this is saying that on the queries coming from Arena users, Gemini wins Claude 3.5 54% of times.

To go into more details, we want to ask, how is this score calculated? A common misconception is that this Elo score is calculated based on online Elo ranking, same as how tennis/chess player's Elo is calculated in the equation below, where all the battles are sorted chronologically and one by one feed into the system for calculation. In the equation below, \(S_A\) is the actual result of the battle, while \(E_A\) is the predicted result from equation (1).

$$ R^{’}_{A} = R_A + K \cdot (S_A - E_A) $$

Chatbot Arena was initially using online Elo system for the ranking with a K-factor of 4, but online Elo system will prefer recent results more than the historical results. This will cause instability in the calculation, for example if you calculate the results twice with reverse ordering, the ranking will become quite different:

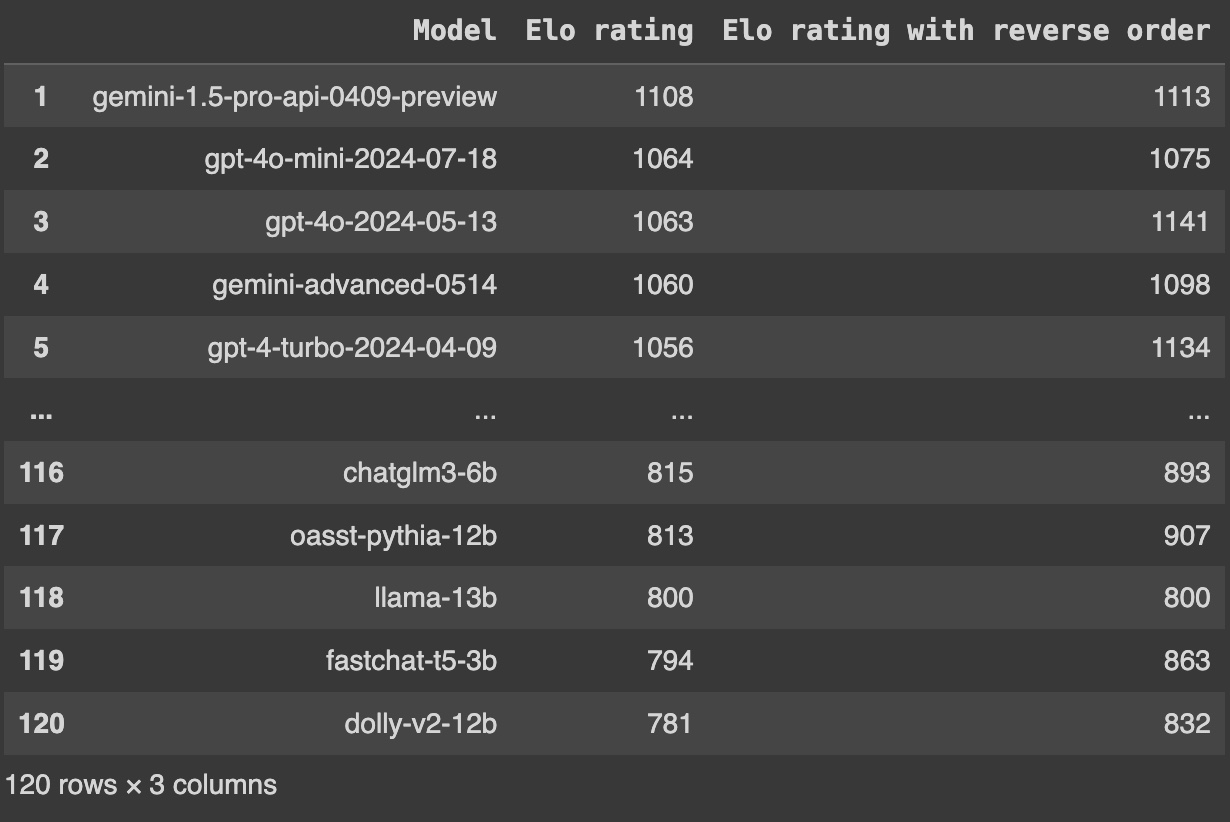
Instead, Chatbot Arena today is using Maximum Likelihood Estimation with Bradley-Terry model to calculate the actual ranking. It reformulates the calculation of the final Elo score into the following MLE problem with logistic regression.

Suppose we have \(M\) models under comparison, and there is no tie. Each model has an Elo estimation \(E\), the base of Elo is \(k\) (\(k=10\) as in the case of equation 1), and scale factor of \(C\) (\(C=400\) in equation (1)) and we have \(T\) observations of the outcome of battle, each denoted as a \(M\) length of vector \(h\) where the ith element has value

$$ h_{t}^{i} = \begin{cases} ln(k) & \text{when ith model is the model a in battle t} \\ -ln(k) & \text{when ith model is the model b in battle t} \\ 0 & \text{when ith model doesn’t participate the battle t} \end{cases} $$

Finally, we let \(y_{1...T}\) be our target ground truth, where

$$ y_{t} = \begin{cases} 1 & \text{when model a is the winner in battle t} \\ 0 & \text{when model b is the winner in battle t} \\ \end{cases} $$

We fit the following logistic regression model with no bias term and \(M\)-length model parameter \(\theta\)

$$ \begin{equation} \begin{aligned} \hat{\theta} &= \argmin_\theta{J(\theta)} \\ &= \argmin_{\theta}-\sum_{t=1}^{T} y_t * \log{\sigma{(h_t \cdot \theta)}} + (1 - y_t) * \log{(1 - \sigma{(h_t \cdot \theta)})} \end{aligned} \end{equation} $$

It's quite easy to prove that the logistic regression coefficient \(\hat{\theta}\) has a deterministic mapping to the optimal ranking Elo score where \(E = C * \hat{\theta}\). We give the rough intuition below.

Suppose we only have a pair of model \(i\) and \(j\), out of all battles, we have \(n\) times model \(i\) wins and \(m\) times it loses. Thus the equation (2) becomes

$$ \begin{aligned} \argmin_{\theta} J &= -n * \log{\sigma{(ln(k) * \theta_i - ln(k) * \theta_j)}} - m * \log{(1 - \sigma{(ln(k) * \theta_i - ln(k) * \theta_j)})} \\ &= -\frac{n}{n+m} * \log{\sigma{(ln(k) * \theta_i - ln(k) * \theta_j)}} - \frac{m}{n+m} * \log{(1 - \sigma{(ln(k) * \theta_i - ln(k) * \theta_j)})} \\ &= -P_{\text{i wins j}} * \log\Bigg[\frac{1}{1 + \exp^{-(ln(k) * \theta_i - ln(k) * \theta_j)}}\Bigg] - (1 - P_{\text{ wins j}}) * \log\Bigg[1 - \frac{1}{1 + \exp^{-(ln(k) * \theta_i - ln(k) * \theta_j)}}\Bigg] \\ &= -P_{\text{i wins j}} * \log\Bigg[\frac{1}{1 + k^{\theta_j - \theta_i}}\Bigg] - (1 - P_{\text{ wins j}}) * \log\Bigg[1 - \frac{1}{1 + k^{\theta_j - \theta_i}}\Bigg] \\ \end{aligned} $$

let \(E = C * \theta\), we then have

$$ \begin{aligned} \argmin_{\theta} J &= -P_{\text{i wins j}} * \log\Bigg[\frac{1}{1 + k^{(E_j - E_i)/C}}\Bigg] - (1 - P_{\text{ wins j}}) * \log\Bigg[1 - \frac{1}{1 + k^{(E_j - E_i)/C}}\Bigg] \\ &= -P_{\text{i wins j}} * \log{\hat{P}_{\text{i wins j}}} - (1 - P_{\text{i wins j}})* \log{(1 - \hat{P}_{\text{i wins j}})} \end{aligned} $$

It’s easy to see that the above equation is to calculate the cross-entropy between the Elo predicted win rate and the actual observed win rate. Thus, the best solution for equation (2) is the Elo score (or MLE coefficient) that predicts exactly the observed win rate.

This calculation is redone N times with bootstrapping to get confidence interval. N equals 100 in the case of the actual Arena implementation.

So what does all these calculation teaches us about the Elo score used in Chatbot Arena?

First, because Bradley-Terry model is used, the model will treat the rating long time ago with the same weight as the it is recently. This might be okay for open source model where static weight is released. But for API based model, such evaluation can be problematic as previous rating is based on weak subversion than the latest most powerful release. That might be why companies like OpenAI and Google is using strange subversion names such as GPT-4o-2024-05-13 instead of just and umbrella version.

Secondly, the score might hide the difference. The plot below is the win rate change as we change the Elo delta.

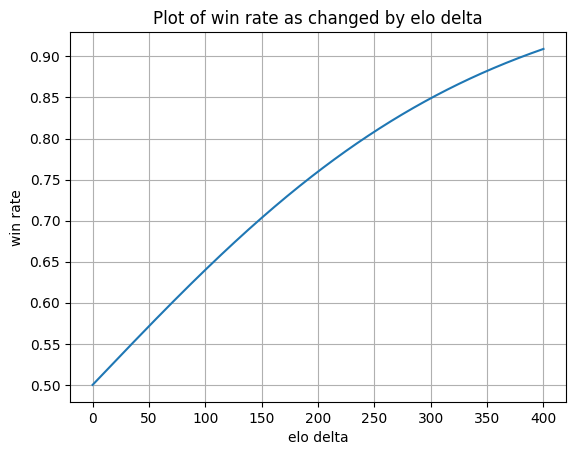
As can be seen here, even a 100 Elo delta renders the win rate from 50% to 65%. When you think about the model difference, I think it’s quite helpful to put it into the context of the actual win rate.

Look Into Different Slice

When you look at the overall slice, the number might suggest that a lot of models are similar. The following graph is a good example of this, this is a snapshot taken earlier this year (not as of time of writing). While it may seems that claude-3-opus is performing worse than llama-3-70b-instruct, when you limit to hard prompt, the performance clearly shows another picture. While the Elo rating is based on the overall uniform sampling of all the ratings, we as user almost always care more about the more challenging prompts. In the end, it doesn’t matter how well your model answers “how are you”, but instead how your model answers “help me translate this C++ program into Haskell”.

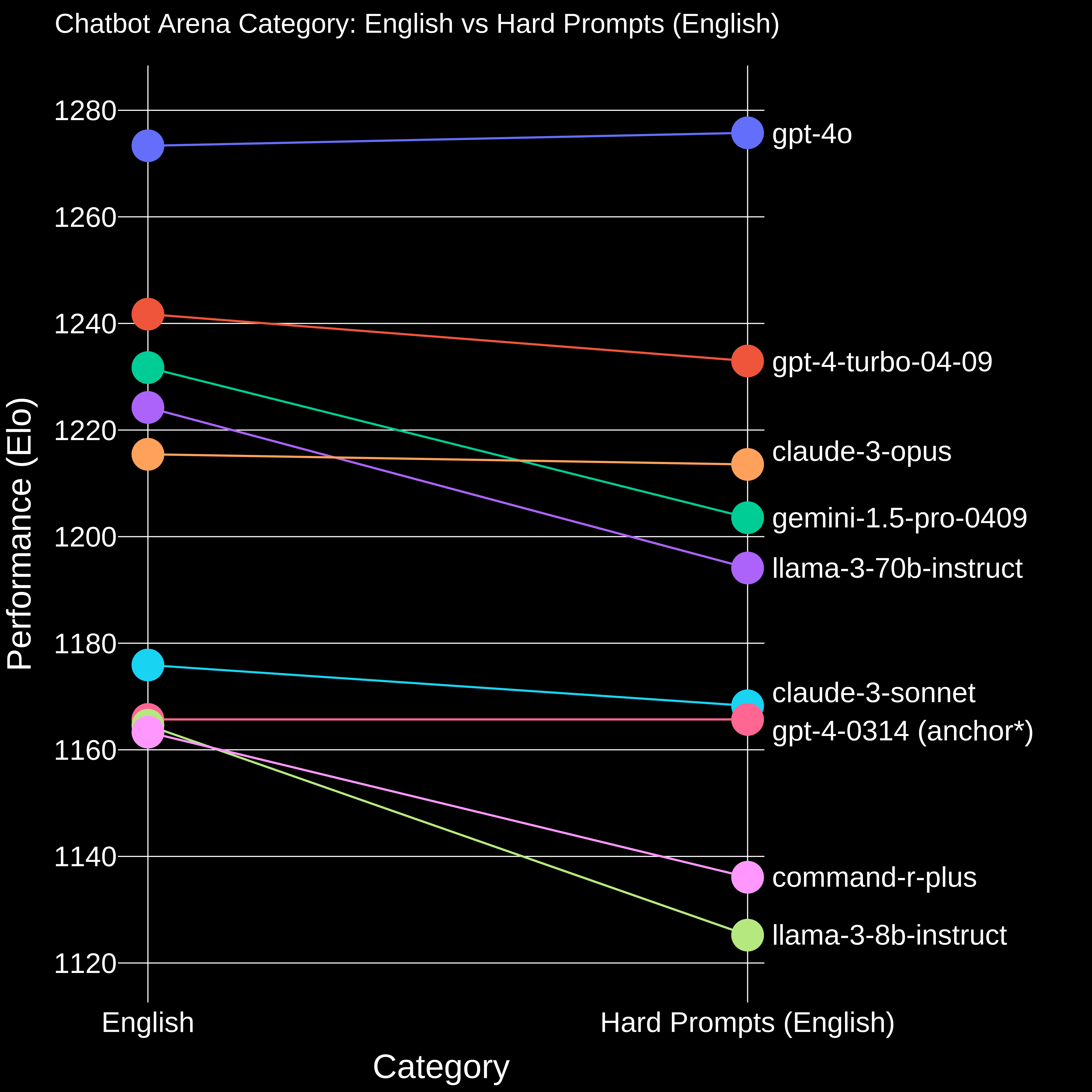
I highly suggest anyone, when picking a model, take a look at the segment that you care about. I suggest definitely take a look at hard and coding, math as these segments correlates with the model’s reasoning capability strongly. For example, while ranked #1 in the overall segment, Gemini-1.5-Pro-Exp-0801’s coding capability significantly lags behind competitors, be careful when you choose it for your coding task.

Summary

I hope this articles provided you more detailed mechanisms for Chatbot Arena. Overall, it’s an open source platform where user across the world assign ratings to chatbot, and one leaderboard that ranks the model’s capability. This simple idea of using communities to help evaluate open-ended prompts turned out to be quite brilliant. But it is not without limitation. The most important limitation is bias, the users that actually coming to this website are majority software engineers and thus shifted this leaderboard heavily towards software engineering. Also the trustworthiness of the rater can be questionable sometimes, although the platform used many mechanisms to detect anormalous users, if you look at some of the safety ratings from the released Arena 33k, clearly the user prefers unsafe content even though the model should moderate sometimes.

But overall, I want you to appreciate the beauty of open source community and the power of simple ideas. Chatbot Arena has become the #1 leaderboard in the LLM industry. I hope this post helps you understand it a bit better!